Rovnice, funkce, kombinatorika, algebraické výrazy... Didaktický test z matematiky se blíží.
Státní maturita z matematiky sice nepatří mezi povinné, řada maturujících jí ale dá přednost před cizím jazykem. Jestli patříš mezi ně, je tenhle článek přesně pro tebe. Shrnujeme v něm, co všechno by se v didaktickém testu mělo objevit, jak by jednotlivé úlohy mohly vypadat a na co si dát u zkoušky pozor, aby ses vyvaroval*a zbytečných chyb.
Co je dobré vědět na začátek?
Didaktický test z matematiky píší maturující, kteří si tento předmět vybrali, jako vůbec první ze všech, tedy 2. května od 8:00. Na zkoušku je vyhrazeno celých 135 minut. Delší čas mohou mít studenti a studentky s tělesným, zrakovým či sluchovým postižením nebo se specifickými poruchami učení, kterým se čas prodlužuje o 25 až 100 procent v závislosti na rozsahu poruchy či postižení.
U zkoušky jsou povolené matematické, fyzikální a chemické tabulky a vzorce pro střední školy, nesmí však obsahovat příklady řešení a vysvětlení vzorců, o osobních poznámkách nemluvě. Je v nich povoleno maximálně zvýraznění či podtržení. Používat mohou maturující i rýsovací potřeby (tužka, guma, pravítko, trojúhelník s ryskou, úhloměr a kružítko) a kalkulačku, k té se ale váže několik pravidel.
Kalkulačka musí být bez grafického režimu, řešení rovnic a úprav algebraických výrazů, nelze použít programovatelnou kalkulačku. Měla by naopak zvládat všechny početní (aritmetické) operace (sčítání, odčítání, násobení, dělení, umocňování a odmocňování) a počítat hodnoty elementárních funkcí (sinus, kosinus a tangens, logaritmus). Toleruje se mnoho dalších funkcí kalkulaček, např. práce se zlomky, částečné odmocňování (tedy úpravy aritmetických výrazů pouze s čísly), převody úhlů, výpočet faktoriálů a kombinačních čísel nebo statistické funkce.
Co všechno v testu bude?
Obsah didaktického testu z matematiky určuje Katalog požadavků platný od školního roku 2015/2016. Jeho hlavní část obsahuje požadavky na konkrétní vědomosti a dovednosti z následujících okruhů:
I. Číselné obory
- Přirozená čísla – provádět aritmetické operace s přirozenými čísly, rozlišit prvočíslo a číslo složené, rozložit přirozené číslo na prvočinitele, rozlišit čísla soudělná a nesoudělná
- Celá čísla – provádět aritmetické operace s celými čísly, užít pojem opačné číslo
- Racionální čísla – užít dekadický zápis čísla, provádět operace se zlomky, provádět operace s desetinnými čísly včetně zaokrouhlování, užívat jednotky a jejich převody, znázornit racionální číslo na číselné ose, porovnávat racionální čísla
- Reálná čísla – užít pojmy opačné číslo a převrácené číslo, znázornit reálné číslo nebo jeho aproximaci na číselné ose, řešit praktické úlohy s mocninami s přirozeným exponentem a odmocninami
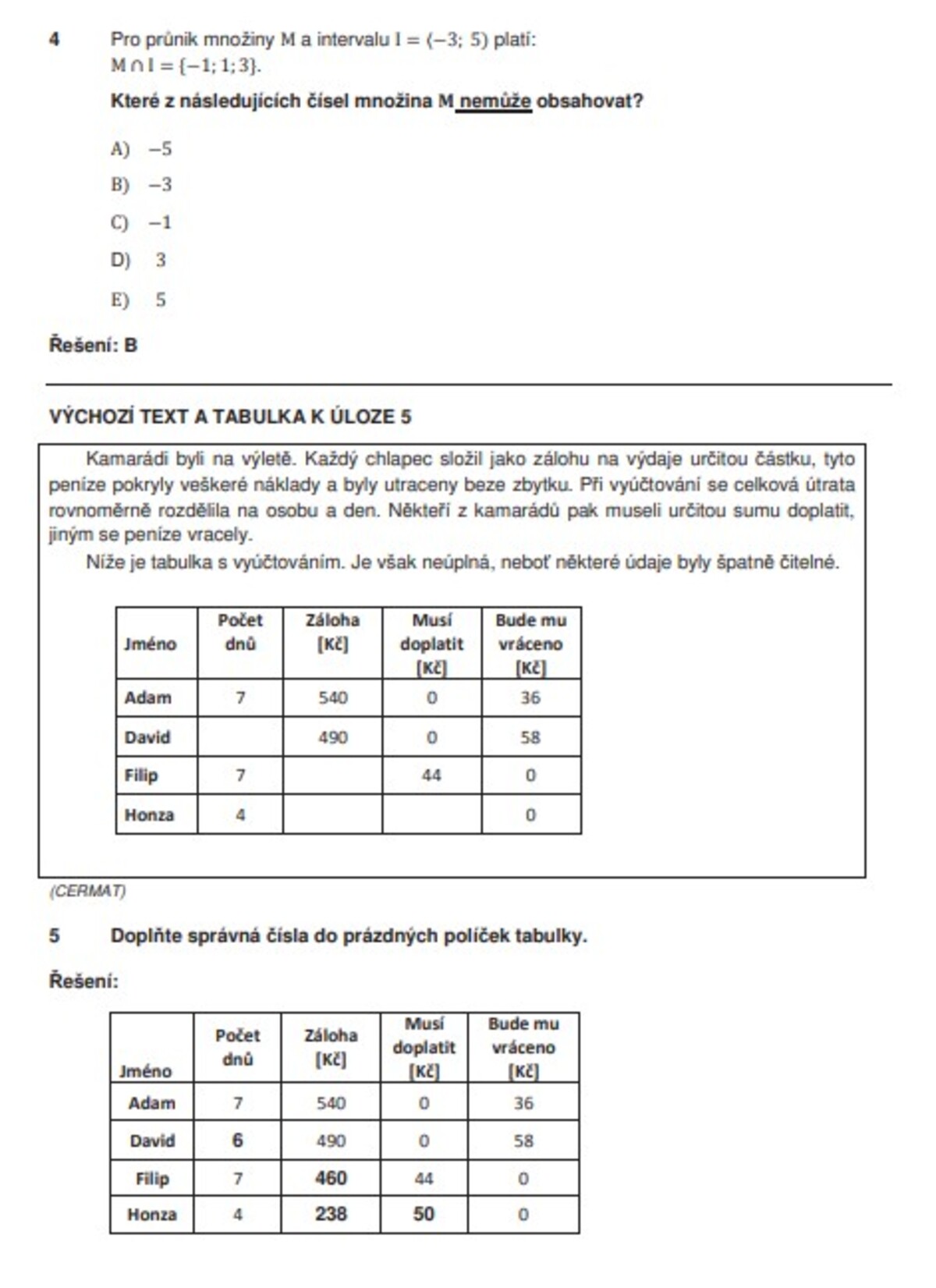
- Číselné množiny – zapisovat a znázorňovat číselné množiny a intervaly, určovat jejich průnik a sjednocení
II. Algebraické výrazy
- Algebraické výrazy – určit hodnotu, nulový bod a definiční obor výrazu, sestavit výraz, interpretovat výraz
- Mnohočleny – užít pojmy člen, koeficient, stupeň mnohočlenu, provádět operace s mnohočleny, provádět umocnění dvojčlenu pomocí vzorců
- Lomené výrazy – provádět operace s lomenými výrazy, určit definiční obor lomeného výrazu
- Výrazy s mocninami a odmocninami – provádět operace s výrazy obsahujícími mocniny a odmocniny, určit definiční obor výrazu s mocninami a odmocninami
III. Rovnice a nerovnice
- Algebraické rovnice a nerovnice – užít ekvivalentní úpravy rovnice a nerovnice, provádět zkoušku
- Lineární rovnice a jejich soustavy – řešit lineární rovnice o jedné neznámé, vyjádřit neznámou ze vzorce, řešit rovnice v součinovém a podílovém tvaru, řešit početně soustavy lineárních rovnic, řešit graficky soustavu dvou lineárních rovnic o dvou neznámých, užít lineární rovnice a jejich soustavy při řešení slovní úlohy
- Kvadratické rovnice – řešit neúplné i úplné kvadratické rovnice a nerovnice, užít vztahy mezi kořeny a koeficienty kvadratické rovnice, užít kvadratickou rovnici při řešení slovní úlohy
- Lineární nerovnice s jednou neznámou a jejich soustavy – řešit lineární nerovnice s jednou neznámou a jejich soustavy, řešit nerovnice v součinovém a podílovém tvaru
IV. Funkce
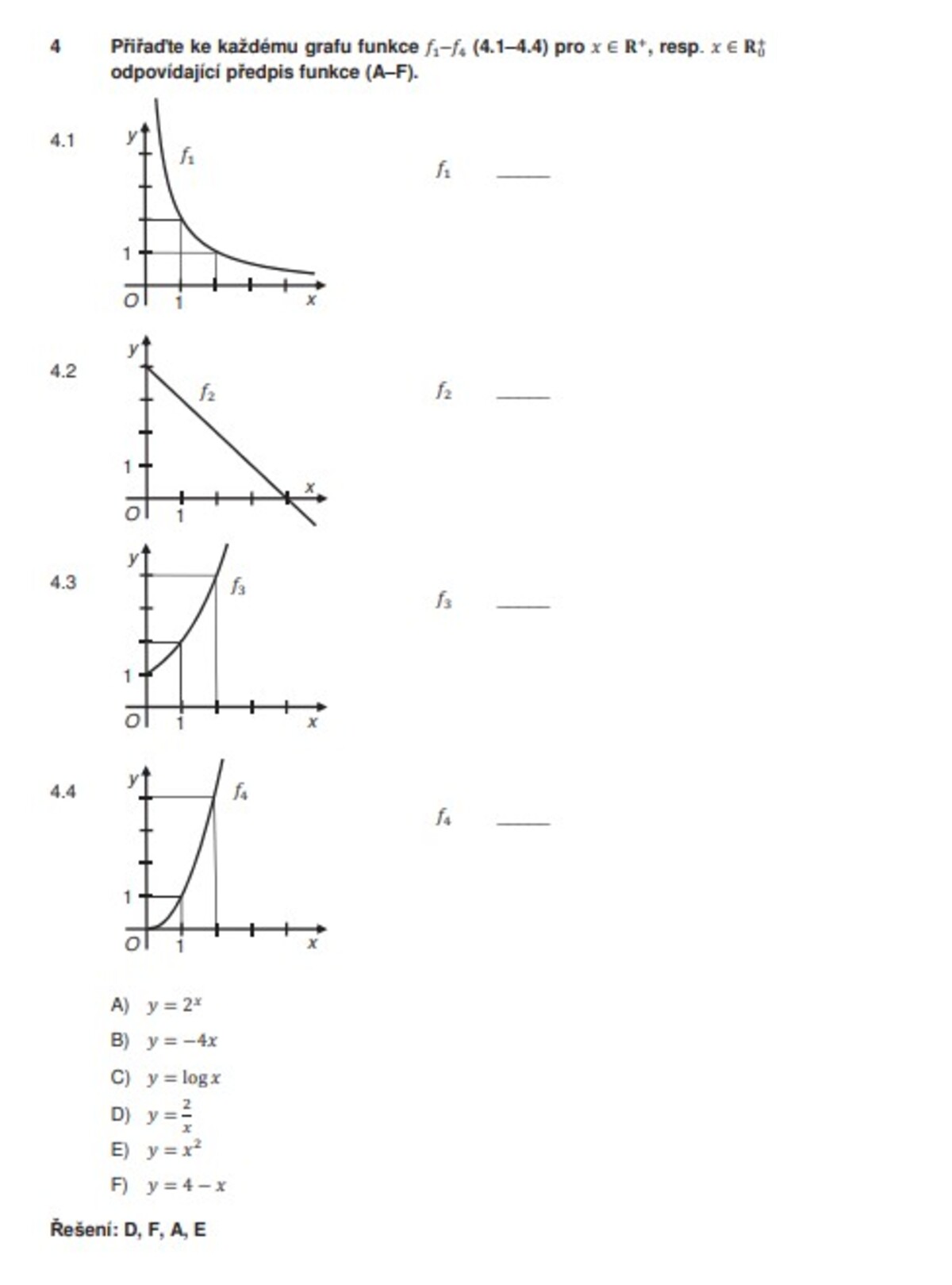
- Základní poznatky o funkcích – sestrojit graf funkce, přiřadit předpis funkce ke grafu funkce a opačně, určit průsečíky grafu funkce s osami soustavy souřadnic, určit z grafu funkce intervaly monotonie
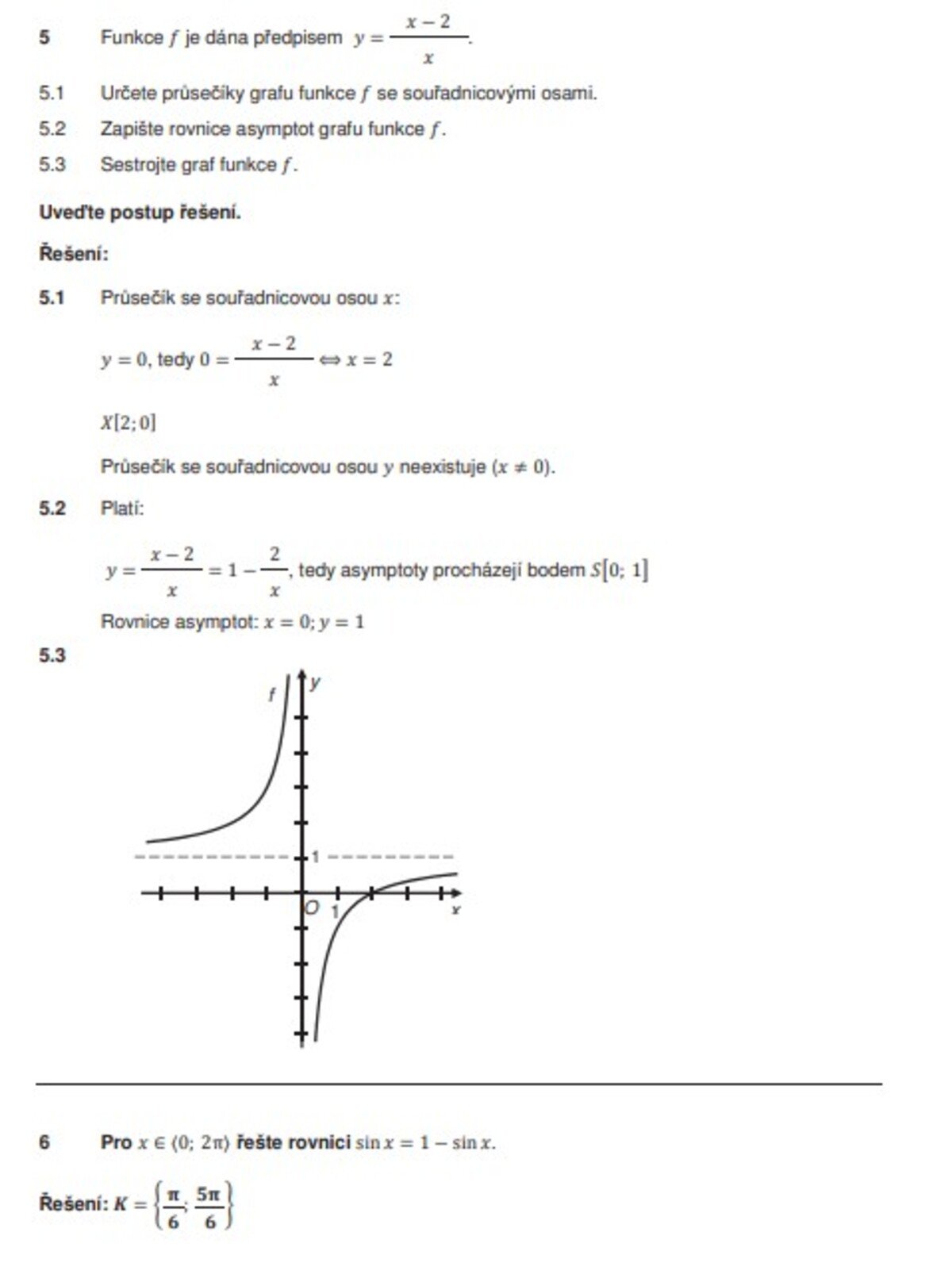
- Lineární funkce, lineární lomená funkce – užít pojem a vlastnosti přímé i nepřímé úměrnosti, sestrojit jejich graf, určit lineární funkci a sestrojit její graf, určit předpis lineární lomené funkce z daných bodů nebo grafu funkce, řešit reálné problémy pomocí lineární funkce a lineární lomené funkce
- Kvadratické funkce – určit kvadratickou funkci, stanovit definiční obor a obor hodnot, sestrojit graf kvadratické funkce, řešit reálné problémy pomocí kvadratické funkce
- Exponenciální a logaritmické funkce – určit exponenciální a logaritmickou funkci, stanovit definiční obor a obor hodnot, sestrojit graf, užít logaritmus, věty o logaritmech, řešit jednoduché exponenciální a logaritmické rovnice
- Goniometrické funkce – užít pojmy orientovaný úhel, velikost úhlu, stupňová míra, oblouková míra a jejich převody, definovat goniometrické funkce v pravoúhlém trojúhelníku, upravovat jednoduché výrazy obsahující goniometrické funkce a stanovit jejich definiční obor
V. Posloupnosti a finanční matematika
- Základní poznatky o posloupnostech – aplikovat znalosti o funkcích při úvahách o posloupnostech a při řešení úloh o posloupnostech, určit posloupnost vzorcem pro ݊n-tý člen, graficky, výčtem prvků
- Aritmetická posloupnost – určit aritmetickou posloupnost a chápat význam diference, užít základní vzorce pro aritmetickou posloupnost
- Geometrická posloupnost – určit geometrickou posloupnost a chápat význam kvocientu, užít základní vzorce pro geometrickou posloupnost
- Využití posloupností pro řešení úloh z praxe, finanční matematika – využít poznatky o posloupnostech při řešení problémů v reálných situacích, řešit úlohy finanční matematiky
VI. Planimetrie
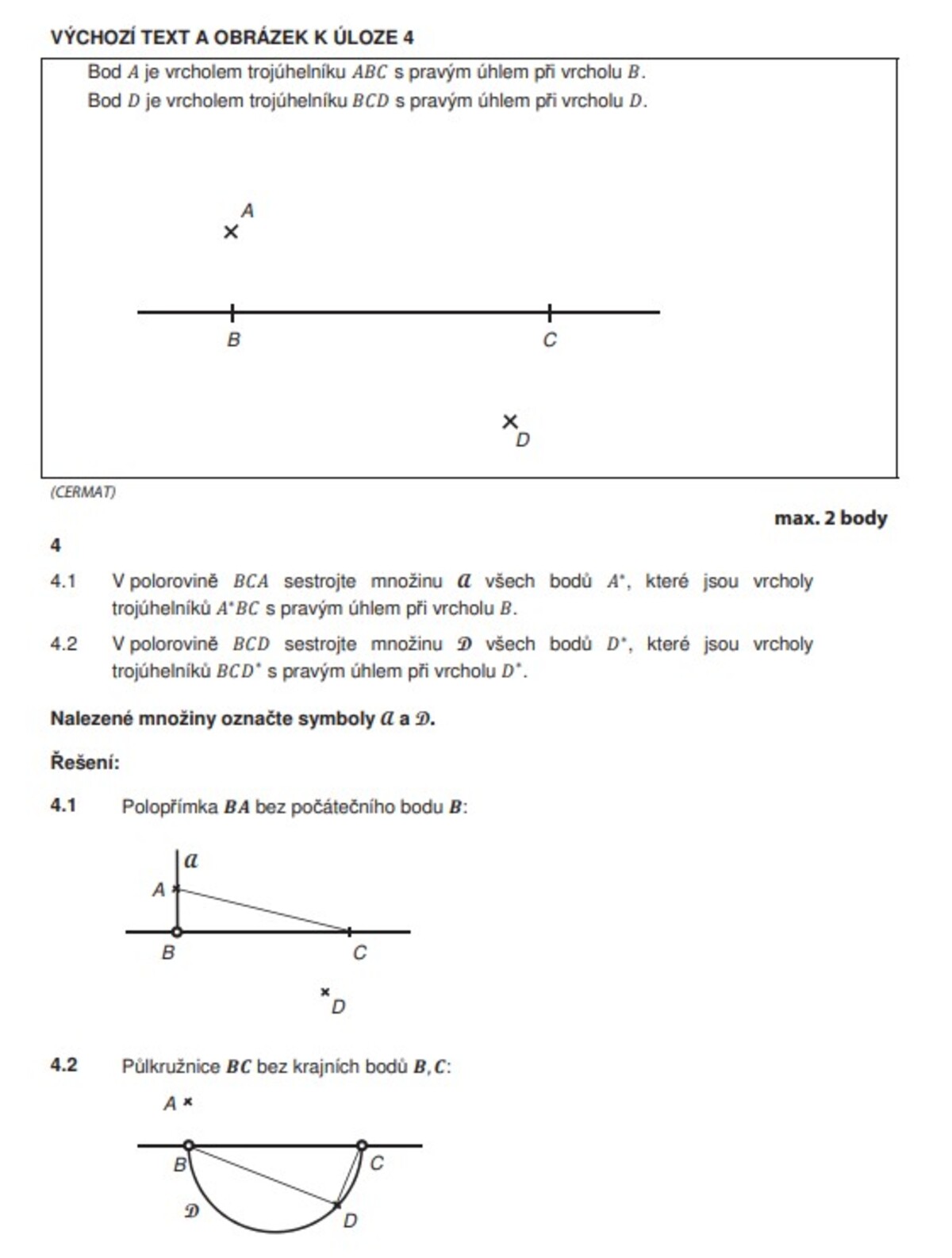
- Planimetrické pojmy a poznatky – užít pojmy bod, přímka, polopřímka, rovina, polorovina, úsečka, úhly (vedlejší, vrcholové, střídavé, souhlasné), objekty znázornit, užít s porozuměním polohové a metrické vztahy mezi geometrickými útvary v rovině (rovnoběžnost, kolmost a odchylka přímek, délka úsečky a velikost úhlu, vzdálenosti bodů a přímek)
- Trojúhelníky – určit objekty v trojúhelníku, znázornit je a správně využít jejich základní vlastnosti, užít s porozuměním poznatky o trojúhelnících (obvod, obsah, velikost výšky, Pythagorova věta, poznatky o těžnicích a těžišti), řešit úlohy s užitím trigonometrie pravoúhlého trojúhelníku a obecného trojúhelníku (sinová věta, kosinová věta).
- Mnohoúhelníky – rozlišit základní druhy čtyřúhelníků, popsat jejich vlastnosti a správně je užívat, užít s porozuměním poznatky o čtyřúhelnících (obvod, obsah, vlastnosti úhlopříček a kružnice opsané nebo vepsané)
- Kružnice a kruh – pojmenovat, znázornit a správně užít základní pojmy týkající se kružnice a kruhu (tětiva, kružnicový oblouk, kruhová výseč a úseč, mezikruží), popsat a užít jejich vlastnosti, užít s porozuměním polohové vztahy mezi body, přímkami a kružnicemi
VII. Stereometrie
- Tělesa – charakterizovat jednotlivá tělesa (krychle, kvádr, hranol, jehlan, rotační válec, rotační kužel, komolý jehlan a kužel, koule a její části), vypočítat jejich objem a povrch, užívat jednotky délky, obsahu a objemu, provádět převody jednotek
VIII. Analytická geometrie
- Souřadnice bodu a vektoru na přímce – určit vzdálenost dvou bodů a souřadnice středu úsečky, užít pojmy vektor a jeho umístění, souřadnice vektoru a velikost vektoru, provádět operace s vektory
- Souřadnice bodu a vektoru v rovině – užít souřadnice bodu v kartézské soustavě souřadnic, určit vzdálenost dvou bodů a souřadnice středu úsečky, provádět operace s vektory (součet, násobek, skalární součin)
- Přímka v rovině – užít parametrické vyjádření přímky, obecnou rovnici přímky a směrnicový tvar rovnice přímky v rovině, určit polohové a metrické vztahy bodů a přímek v rovině a aplikovat je v úlohách
IX. Kombinatorika, pravděpodobnost a statistika
- Základní poznatky z kombinatoriky a pravděpodobnosti – užít základní kombinatorická pravidla, počítat s faktoriály a kombinačními čísly, užít s porozuměním pojmy náhodný pokus, výsledek náhodného pokusu, náhodný jev, opačný jev, nemožný jev a jistý jev
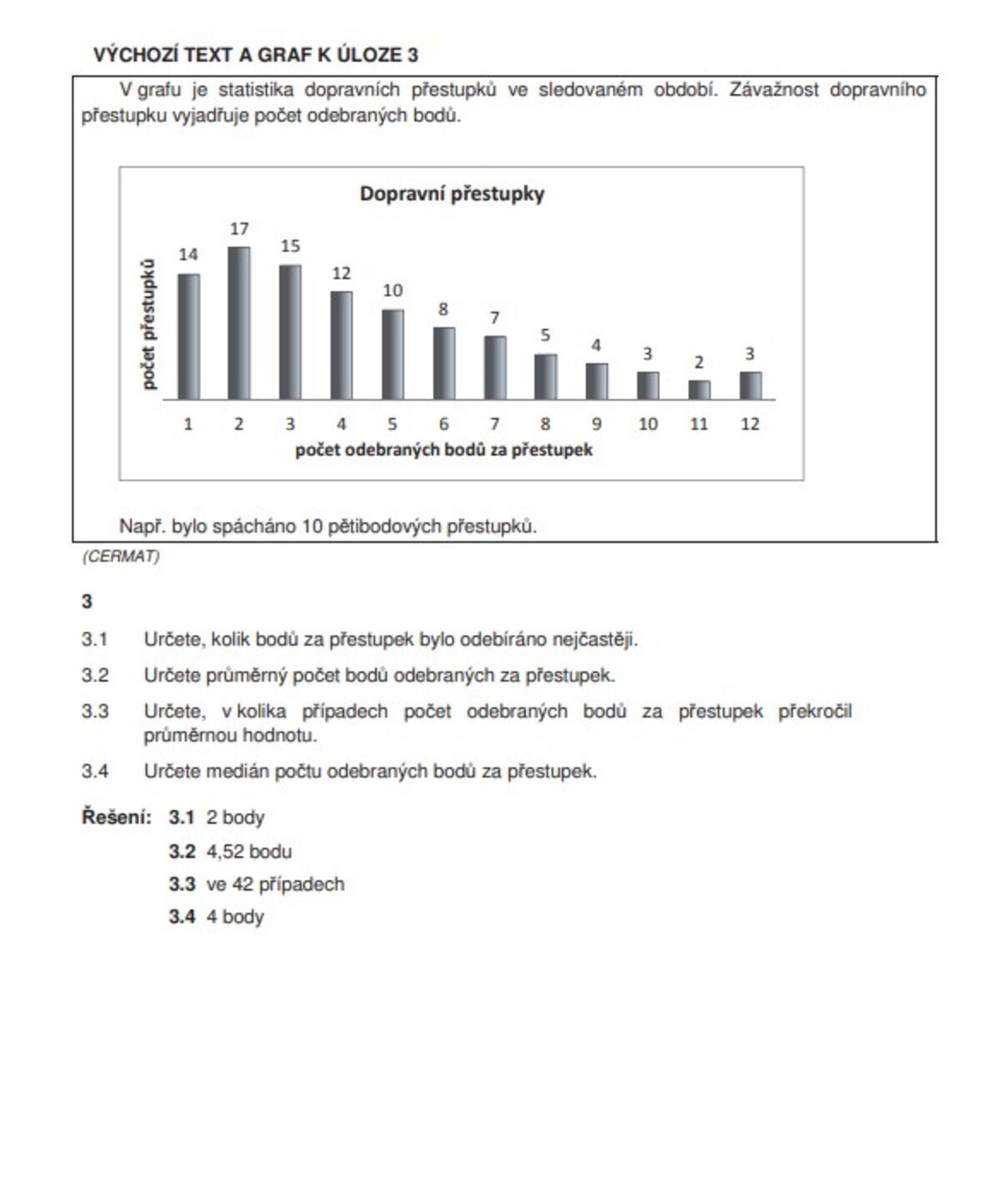
- Základní poznatky ze statistiky – užít pojmy statistický soubor, rozsah souboru, statistická jednotka, statistický znak kvalitativní a kvantitativní, hodnota znaku a pojmy vysvětlit, vypočítat četnost a relativní četnost hodnoty znaku, sestavit tabulku četností, graficky znázornit rozdělení četností, určit charakteristiky polohy (aritmetický průměr, medián, modus, percentil) a variability (rozptyl a směrodatná odchylka)
| Tematické okruhy | Zastoupené v testu (v %) |
| I. Číselné množiny | 4–12 |
| II. Algebraické výrazy | 8–18 |
| III. Rovnice a nerovnice | 12–20 |
| IV. Funkce | 10–20 |
| V. Posloupnosti a finanční matematika | 4–14 |
| VI. Planimetrie | 8–18 |
| VII. Stereometrie | 4–12 |
| VIII. Analytická geometrie | 4–14 |
| IX. Kombinatorika, pravděpodobnost a statistika | 4–14 |
Jak je test hodnocený a kolik bodů potřebuješ na úspěšné absolvování?
Didaktický test z matematiky se hodnotí slovně hodnocením „uspěl“ nebo „neuspěl“. Za správná řešení všech úloh v testu lze získat celkem 50 bodů, pro úspěšné složení zkoušky je potřeba získat alespoň 17 bodů. Testy se hodnotí centrálně a výsledky dostanou školy do 15. května.
Na co si dát pozor?
Matematika bohužel není předmět, který se dá naučit během pár dní. Většinou si ho vybírají studenti a studentky, u kterých se předpokládá, že tomuto předmětu základně rozumí. I u nich ale může být důvodem neúspěchu neporozumění otázkám a úkolům. Nejlépe se na test tedy připravíš tak, že si budeš zkoušet úlohy z minulých let. U samotného testu pak můžeš začít první otázkou a pokračovat dál, případně začít otázkami, u kterých si jsi jistější, a k těm složitějším se pak vrátit. Stejně jako u všech ostatních testů se vyplatí číst pozorně zadání, odpovědi do archu zaznamenávat čitelně a vše si po sobě zkontrolovat.