Hilbertův paradox o nekonečném hotelu aneb všechna nekonečna nejsou stejná

Letní prázdniny se (naštěstí) velmi rychle přibližují a s nimi jsou spojeny i dovolené a ubytování v různých hotelech. Komu by se nelíbil pětihvězdičkový hotel na pláži na vašem vysněném místě? Přesto se dnes nebudeme věnovat cestovnímu ruchu ani ubytování, ale něčemu, co fascinuje lidi už odedávna - nekonečno.
 
Němec David Hilbert (1862 - 1943) byl jedním z nejzaslouženějších matematiků tehdejší doby. Kromě mimořádného úspěchu na mnoha polích pronesl něco, co se dnes označuje jako Hilbertův paradox. Díky němu zjednodušil pojem nekonečna a v hlavě si postavil opravdu velký hotel.

Nekonečno

Nejprve však pár jednoduchých faktů o nekonečnu. Je zajímavé, že se o něm každý vyjadřuje jako o čísle, ale na číselné ose se zkrátka nenachází. Víme jen, že je někde daleko vpravo na konci osy a pak ještě kousek. No a to je první chyba. Nekonečno je číselná osa celá - všechna ta celá čísla jako 5, 6, 7, 8..., je jich tam zkrátka nekonečno. To je první nekonečno, o kterém můžeme spolehlivě říci, že nemá konec, protože ať napíšeme jakékoli číslo, můžeme k němu vždy přidat jedničku (n+1). Mimochodem, tomuto typu nekonečna se říká spočitatelné nebo "countable infinity".

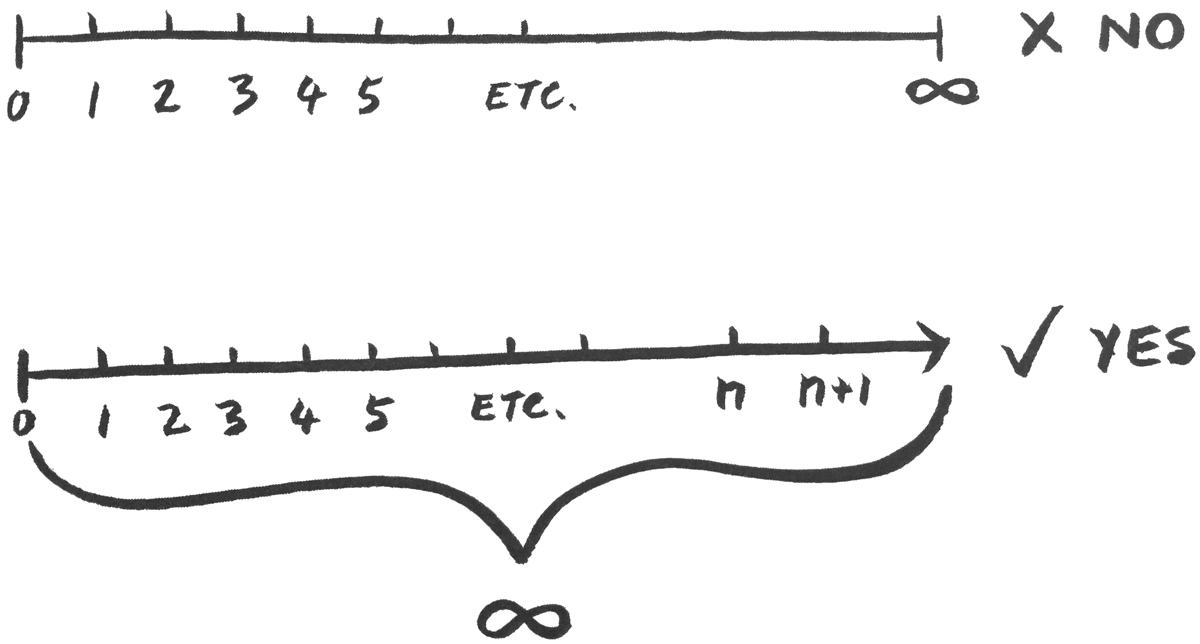
Určitě každého teď napadne, že existuje ještě více hardcore level nekonečna. Na číselné ose jsou mezi celými čísly prázdné kousky, ve kterých jsou čísla s desetinnou čárkou. A těch je tam nekonečno. V nekonečném počtu prázdných kousků mezi dvěma celými čísly. To se zdá jako nekonečno² aneb nekonečno^nekonečno ale to, že jde jen o to běžné nekonečno, vysvětlíme později.
 
My si však dovolíme ještě přilít do ohně a zeptáme se - napiš všechna čísla od nuly. První bude tedy nula. Ale co následuje? Bude to 0.0001? Nebo snad 0.00000001? Možností je nekonečno. Toto je zase nelze nespočitatelné nekonečno, nebo kontinuum.
 
Na závěr krátkého informačního okénka ještě poslední věc a pak už bude hotel, slibujeme. Pokud máš hromádku 7 bonbonů a jeden tam přidáš, máš jich 8, to by měla většina lidí akceptovat. Pokud máš nekonečno bonbónů a k tomu přidáš bonbón, nemáš ∞ + 1 bonbónů, ale pouze ∞, protože jak jsme si ukázali výše, nekonečno není číslo, nelze k němu přidávat. Detto ∞ krát ∞ je stále ∞.

Nekonečný hotel

Strýček Hilbert má hotel s nekonečným počtem pokojů a ubytovává nekonečný počet hostů. Dvě nekonečna jsou si rovna, a tedy v každém pokoji je jeden host. Pokoje jsou označeny čísly (1, 2...) a všichni hosté jsou spokojeni, ale v tom na dveře zaklepe muž, který chce další pokoj. Co teď? Vždyť všechny pokoje jsou obsazeny, každé číslo má svého hosta. Konec chodby s pokoji není a Hilbert kvůli tomu nemá jak nového hosta poslat na konec chodby. S potenciálním zákazníkem to moc dobře tedy nevypadá. Ale strýček Hilbert je slavný matematik a vymyslí to. Ubytovaného z pokoje 1 přesune do dvojky, hosta z pokoje 2 do pokoje 3 a takto se celý hotel přestěhuje. Počet pokojů je stále nekonečný, počet hostů je nekonečný a pravděpodobně bude nekonečný i počet stížností ubytovaných na tento nekonečně skvělý byznys.
 
Jednoho hosta tedy Hilbert ubytuje a ubytoval by i další příchozí. Zkrátka by všechny hosty posunul dál. Co když však přijde dovolenkový autobus s nekonečným počtem hostů? Ten totiž právě zaparkoval a tak je třeba velmi rychle vymyslet řešení, jak ubytovat další nekonečno lidí.
 
Už jsme zmínili, že počitatelná nekonečna jsou stejná, a tedy ubytované nekonečno, nekonečno, které se chce dát ubytovat a i finální nekonečno by měla být stejná. Teoreticky by se to tedy mělo dát zvládnout. Nejprve si však dovolíme návrat k informačnímu okénku a zeptáme se: Kolikrát je všech kladných celých čísel více než všech sudých čísel?
 
Zdravý rozum a i vše ostatní křičí, že sudých čísel je přece dvakrát méně, bohužel je to opět špatně. Ani seznam kladných, ani seznam sudých čísel nemají konec, takže jsou obě nekonečná - tedy shodná. Čili existuje stejně sudých čísel jako stejně všech celých čísel. Mindblown.

Hilbert o tomto tuší, a tak přesune každého hosta do pokoje s číslem dvakrát větším než je aktuální číslo ubytovaného. Pan z dvojky jde na čtyřku atd. Tím pádem se uvolní polovina všech pokojů, kam nacpeme to nekonečno, které právě vystupuje z autobusu. Mimochodem, opravdu bychom nechtěli bydlet v pokoji s číslem 682779 a stěhovat se do dvakrát většího čísla.
 
Hilbert je zřejmě opravdu matematickým a logickým bohem, ale chuť zákazníků ubytovat se v jedinečném nekonečném hotelu ještě stoupla, a tak na parkovišti zastavilo nekonečno autobusů s nekonečným počtem hostů. Protože v minulém příkladu přišlo jen nekonečno, domácí musel vytvořit nekonečno pokojů. Zde je však třeba vytvořit nekonečno nekonečen pokojů a strýček Hilbert se už pořádně potí. Proto zavolá svým dvěma dobrým přátelům - Georgovi Gamowovi a Albertu Einsteinovi. Společně přijdou na to, že to opravdu jde. Už se nacházíme v době, kdy víme, že prvočísel (číslo dělitelné pouze 1 a sebou samým) je nekonečno. Mocniny prvočísla mají tu pěknou vlastnost, že pak už nejsou mocninou dalšího jiného čísla. Tedy například druhá mocnina čísla 11 je 121 a ta se nedá odmocnit do jiného celého čísla kromě jedenáctky.

Hilbert tedy umístí všechny již ubytované hosty do pokojů, jejichž čísla jsou mocninou prvního prvočísla. To je dvojka, zákazníci se přesunou do pokojů 2, 4, 8, 16, 32.... První autobus z nekonečna umístí do pokojů, které jsou mocninou druhého prvočísla v řadě, to je trojka. Obsazeny jsou tedy pokoje 3, 9, 27, 81... Další prvočíslo je 5, tedy se obsadí pokoje 5, 25, 125... A tak dále.
 
A tady celý myšlenkový experiment vystupující pod názvy Hilbertův paradox, Hilbert Grand Hotel nebo prostě Nekonečno pokojů, končí. Hilbert ukázal, že všechna počitatelná nekonečna jsou stejná a jakákoliv manipulace s nimi vždy ústí do nekonečna. David Hilbert zemřel v roce 1943 v Německém Göttingenu, ale jeho důmyslnost slouží dodnes každému z nás.

První dvě zákaznické vlny elegantně vysvětlí i video, anglicky.